SWEA 12090. 칩 생산
많이 어려운 문제
$~$
정말 많은 걸 고려해야 하는 문제이다. 우선, 기본적으로 완전 탐색 문제이다.
세로가 10, 가로가 25이하이기 때문에 2x2 칩은 최대 60개가 가능하다. 해당 영역을 선택하느냐 하지 않느냐로 구분하면 칩 하나당 2가지 선택 방법이 있고, 60개가 존재할 수 있기 때문에 경우의 수는 ${2^{60}}$ 이다. 문제의 제한 조건을 보면 50개의 테스트 케이스를 합쳐 3초(3억 연산)이기 때문에 평균 테스트 케이스당 6백만 연산이어야 한다. 완전 탐색은 시간 초과가 발생할 것이 자명하기 때문에 다른 알고리즘을 찾아보거나 최적화를 해야 한다.
최적화의 방법으로 memoization이 있다. memoization의 방법으로는 다음과 같이 마지막 row - 1까지 탐색한 후 계속 재귀 호출을 종료해가는 과정에서 n번째 row에 대해 가로 길이-1(가로 2인 칩이기 때문)까지 탐색한 상태일 때 마지막 row까지 탐색했던 결과를 저장하는 것이다. 그렇게 되면 앞으로 되돌아갔다가 다시 n번째 row에 대해 가로 길이-1까지 탐색을 동일하게 한 후 n+1 row 탐색해야 할 때 해당 과정을 다시 반복할 필요가 없어져 시간 단축을 할 수 있다.
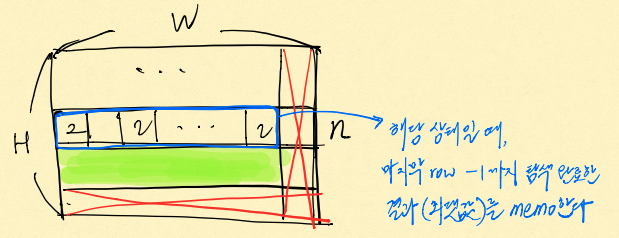
그리고 문제에서 가로의 최대 길이가 25이고 세로의 최대 길이가 10인데, 가로로 짧은 상태가 memoization에서 더 빈번하게 이미 memo된 값을 참조하게 되기 때문에 가로와 세로를 변경해준다.
row의 상태는 bitmasking을 통해 나타낼 수 있고, 각 row에 대한 row의 상태가 필요하기 때문에 2차원 배열이여야 한다. 크기를 나타내면 ${ {세로 길이} \times 2^{가로 길이} }$이고, 실제 수로는 ${25\times 2^{10} }$이다. 문제의 제한 조건인 256MB 이하이다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
import java.util.*;
import java.io.*;
public class Solution {
static int N, M;
static int[][] visited = new int[26][11];
static int[][] board = new int[26][11];
static int[][] memo = new int[25][(1 << 10) + 1]; // [row][rowState]
static int res = 0;
static int[] dx = {0, 0, 1, 1};
static int[] dy = {0, 1, 1, 0};
// 영역을 선택하는 메서드(왼쪽 상단은 2로 설정, 나머지 3 곳은 1로 설정)
static void setSquare(int r, int c) {
visited[r][c] = 2;
for (int i = 1; i < 4; i++)
visited[r+dx[i]][c+dy[i]] = 1;
}
// 선택한 영역을 되돌리는 메서드
static void clearSquare(int r, int c) {
for (int i = 0; i < 4; i++)
visited[r+dx[i]][c+dy[i]] = 0;
}
// 해당 영역 선택이 가능한 지 확인하는 메서드
static boolean possible(int r, int c) {
if (c >= M-1) return false;
for (int i = 0; i < 4; i++)
if (board[r+dx[i]][c+dy[i]] == 1) return false;
for (int i = 0; i < 4; i++)
if (visited[r+dx[i]][c+dy[i]] != 0) return false;
return true;
}
// 해당 row 상태를 얻는 메서드
static int getRowState(int r) {
int rowState = 0;
for (int j = 0; j < M-1; j++) {
rowState <<= 1;
if \(visited\[r]\[j] == 2) rowState |= 1;
}
return rowState;
}
// 재귀
static int go(int idx) {
int r = idx / M;
int c = idx % M;
// 종료 조건
if (r == N-2 && c == M-1) return 0;
int rowState = 0;
// col 끝에 도달하면 이미 방문한 rowState 상태인지 확인
if (c == M-1) {
rowState = getRowState(r);
if (memo[r][rowState] != -1) return memo[r][rowState];
}
int max = 0;
// 영역 선택하기
if (possible(r, c)) {
setSquare(r, c);
int ret = go(idx + 1);
max = Math.max(max, ret + 1);
clearSquare(r, c);
}
// 영역 선택 안 하기
int ret = go(idx+1);
max = Math.max(max, ret);
// memo하기
if (c == M - 1)
memo[r][rowState] = max;
return max;
}
public static void main(String[] args) throws Exception {
BufferedReader in = new BufferedReader(new InputStreamReader(System.in));
int testcase = Integer.parseInt(in.readLine());
for (int tc = 1; tc <= testcase; tc++) {
for (int i = 0; i < N; i++)
Arrays.fill(memo[i], -1);
StringTokenizer st = new StringTokenizer(in.readLine(), " ");
M = Integer.parseInt(st.nextToken());
N = Integer.parseInt(st.nextToken());
for (int c = 0; c < M; c++) {
st = new StringTokenizer(in.readLine(), " ");
for (int r = 0; r < N; r++) {
board[r][c] = Integer.parseInt(st.nextToken());
}
}
res = go(0);
System.out.println("#" + tc + " " + res);
}
}
}