0. 개요

1. 삽입 정렬(Insertion sort)

  • 정렬되어 있는 배열에 아직 정렬되지 않은 원소의 들어갈 위치를 찾아 삽입하는 정렬
  • 정렬되어 있을 때 가장 효율이 높다. 정렬되어 있는 배열의 가장 끝에 있는 원소만 정렬되지 않은 원소와 비교하면 되기 때문이다. O(N)
  • 시간 복잡도
    • 평균 : O(N^2)
    • 최선 : O(N)
    • 최악 : O(N^2)

1.1. 코드

// 오름차순 정렬
void insertionSort(int arr[], int N) {
	for (int i = 1; i < N; i++) {
		int key = arr[i];
		for (int j = i-1; j >= 0; j--) {
			if (key < arr[j])
				arr[j+1] = arr[j];
			else
				break;
		}
		arr[j+1] = key;
	}
}

1.2. 이진 삽입 정렬(Binary insertion sort)

삽입 정렬에서 정렬되지 않은 원소의 들어갈 위치를 찾을 때, [[binary-search]]{이진 탐색(binary search)}을 활용하는 정렬. 삽입 정렬에서 살짝 개선된 것

1.2.1 코드

void binaryInsertionSort(int arr[], int N) {
	for (int i = 1; i < N; i++) {
		int key = arr[i];
		
		int start = 0;
		int end = i - 1;
	
		int mid;
		while (start < end) {
			mid = (start + end) / 2;
			if (key >= mid)
				start = mid + 1;
			else
				end = mid;
		}
	}
}

2. 선택 정렬(Selection sort)

  • 매번 그 때의 가장 작은(큰) 원소의 index를 찾아내어 현재 index의 원소와 swap하는 정렬
  • 시간 복잡도
    • 평균 : O(N^2)
    • 최선 : O(N^2)
    • 최악 : O(N^2)

2.1 코드

void selectionSort(int arr[], int N) {

	// 마지막 숫자는 자동으로 정렬되기 때문에 (숫자 개수-1) 만큼 반복한다.
	for(int i = 0; i < N-1; i++) {
		int minIndex = i;

		// 최솟값을 탐색한다.
		for(int j = i+1; j < N; j++) {
			if(arr[j] < arr[minIndex])
				minIndex = j;
		}

		// 최솟값이 자기 자신이면 swap 하지 않는다.
		if(i != minIndex)
			swap(arr[i], arr[minIndex]);
	}
}

3. 버블 정렬(Bubble sort)

  • 서로 인접한 두 원소를 검사하여 정렬하는 알고리즘
  • 인접한 2개의 레코드를 비교하여 크기가 순서대로 되어 있지 않으면 swap한다.
  • 시간 복잡도
    • 평균 : O(N^2)
    • 최선 : O(N^2)
    • 최악 : O(N^2)

3.1 코드

void bubble_sort(int arr[], int N){
	for(int i = N-1; i > 0; i--) {
		for(j=0; j < i; j++) {
			// j번째와 j+1번째의 요소가 순서대로 되어 있지 않으면 swap
			if(list[j] < list[j+1]) {
				swap(arr[j], arr[j+1]);
			}
		}
	}
}

4. 퀵 정렬(quick sort)

  • pivot의 위치를 찾아가면서 진행되는 정렬 알고리즘
    • pivot보다 작은 혹은 큰 원소의 개수만 알면 pivot의 최종 위치를 알 수 있다.
  • 일반적으로 가장 빠른 정렬
  • 이미 정렬되어 있을 경우 O(N^2)로, 효율이 가장 낮다.
    • 재귀 함수가 1과 N-1, N-1이 다시 1과 N-2, … 분할이 N만큼 일어난다.
    • N-1 + N-2 + N-3 + … + 1 = (N-1)*N/2   =>   O(N^2)
  • [[divide-and-conquer]]{분할 정복(divide and conquer)} 방법으로 구현된다.(재귀 함수)
  • in-place 정렬 알고리즘(그 자리에서 값을 바꾸는 알고리즘)
  • cache hit rate가 좋다.
    • pivot을 이용하므로 시간 지역성 높고, 순차적으로 배열에 접근하면서 비교하기 때문에 공간 지역성이 높다.
  • 시간 복잡도
    • 평균 : O(NlogN)
    • 최선 : O(NlogN)
    • 최악 : O(N^2)
  • 공간 복잡도 : O(logN) ~ O(N)
    • 퀵 정렬에서는 재귀적인 호출을 이용하기 때문에 스택을 관리하기 위한 메모리가 별도로 필요하다. 스택에 소모되는 메모리는 재귀 함수의 깊이와 비례하게 된다. 그러므로 분할이 이상적으로 이루어진 경우 O(logN)의 스택 메모리가 소요된다. 최악의 경우, 즉 분할이 한쪽으로만 이루어진 경우에는 O(N)의 스택 메모리가 필요하다

4.1. 코드

정해진 pivot보다 작은(또는 큰) 원소가 몇 개인지 알면 해당 pivot에 해당하는 원소가 정렬했을 때 몇 번째 위치인지 알 수 있다.
아래의 코드는 오름차순 정렬이다. left가 start+1부터 시작하게 되면 원소가 2개인 경우에 문제가 발생하기 때문에, start부터 시작하게 된다.

while (arr[left] <= pivot && left < end)에만 left < end 조건이 있는 이유는 while(pivot < arr[right])에서는 항상 right가 pivot위치에 가게 되면 해당 while이 종료되기 때문이다.

결국 최상위 while이 종료된 후의 right는 항상 pivot보다 작거나 같은 값을 갖는 부분 집합의 마지막 index를 가리키게 된다. 그리고 최상위 while문 밖에서 pivot의 위치인 start와 right(pivot보다 작거나 같은 값을 갖는 부분 집합의 마지막 index)와 swap하게 되고, pivot 양쪽으로 재귀 함수를 호출한다.

void quickSort(int arr[], int start, int end) {
	if (start >= end) return;

	int pivot = arr[start];

	int left = start;
	int right = end;

	while (left < right) {
		while (arr[left] <= pivot && left < end)
			left++;
		while (pivot < arr[right])
			right--;

		if (left < right)
			swap(arr[left], arr[right]);
	}

	swap(arr[start], arr[right]);

	quickSort(arr, start, right - 1);
	quickSort(arr, right + 1, end);
}

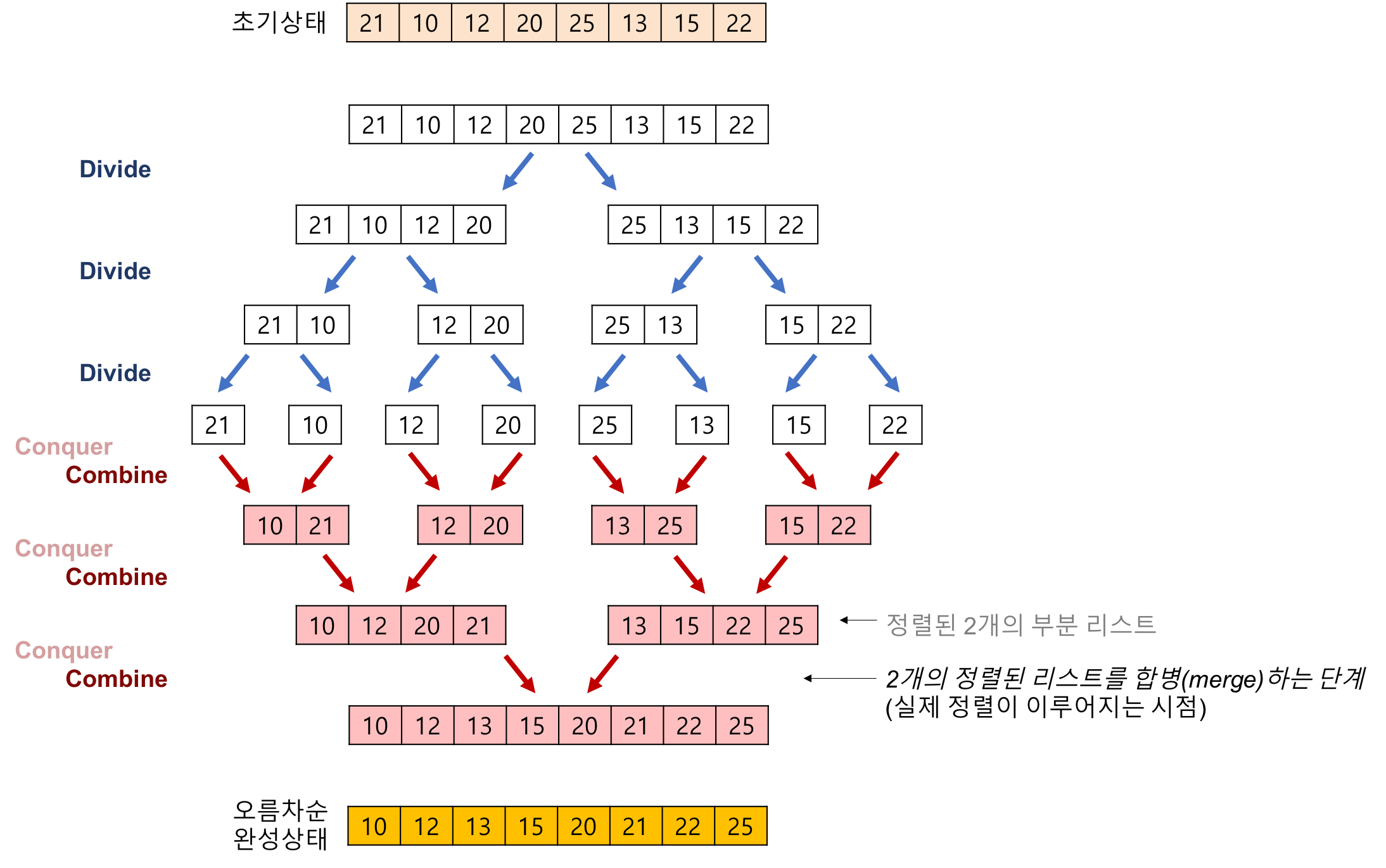
5. 합병 정렬(Merge sort)

  • [[divide-and-conquer]]{분할 정복(divide and conquer)} 방법으로 구현된다.(재귀 함수)
  • 결합 : 두 개의 배열을 순서에 맞게 하나의 배열로 합치는 과정
  • in-place 정렬 알고리즘(그 자리에서 값을 바꾸는 알고리즘)
  • 시간 복잡도
    • 평균 : O(NlogN)
    • 최선 : O(NlogN)
    • 최악 : O(NlogN) 1 

int sorted[MAX_SIZE] // 추가 공간

// i: 정렬된 왼쪽 리스트에 대한 인덱스
// j: 정렬된 오른쪽 리스트에 대한 인덱스
// k: 정렬될 리스트에 대한 인덱스
/* 2개의 인접한 배열 arr[left...mid]와 arr[mid+1...right]의 합병 과정 */
/* (실제로 숫자들이 정렬되는 과정) */
void merge(int arr[], int left, int mid, int right) {
	int i, j, k;
	i = left;
	j = mid + 1;
	k = left;

	/* 분할 정렬된 arr의 합병 */
	while(i <= mid && j <= right) {
		if(arr[i] <= arr[j])
			sorted[k++] = arr[i++];
		else
			sorted[k++] = arr[j++];
	}

	// 남아 있는 값들 일괄 복사
	while (i <= mid)
		sorted[k++] = arr[i++];

	while (j <= right)
		sorted[k++] = arr[j++];
		
	for(i = left; i <= right; i++)
		list[i] = sorted[i];
}

// 합병 정렬
void mergeSort(int arr[], int left, int right) {
	if (left == right) return;

	int mid = (left + right)/2; // 중간 위치를 계산하여 리스트를 균등 분할 -분할(Divide)
	mergeSort(arr, left, mid); // 앞쪽 부분 리스트 정렬 -정복(Conquer)
	mergeSort(arr, mid+1, right); // 뒤쪽 부분 리스트 정렬 -정복(Conquer)

	merge(arr, left, mid, right); // 정렬된 2개의 부분 배열을 합병하는 과정 -결합(Combine)
}

6. 힙 정렬(Heap sort)

  • heap
    • 최솟값 혹은 최댓값이 root에 존재하는 완전 이진 트리
    • 부모 노드의 키 값이 자식 노드의 키 값보다 크거나 같은 완전 이진 트리
    • 우선순위 큐로 구현
  • heap의 특성을 계속 유지하는 정렬(전체 자료를 정렬하는 것이 아니다)
  • 삽입
    • 힙에 새로운 요소가 들어오면, 일단 새로운 노드를 힙의 마지막 노드에 삽입한다.
    • 새로운 노드를 부모 노드들과 교환해서 힙의 성질을 만족시킨다.
      https://gmlwjd9405.github.io/images/data-structure-heap/maxheap-insertion.png
  • 삭제
    • 최대 힙에서 최댓값은 루트 노드이므로 루트 노드가 삭제된다.
      • 최대 힙(max heap)에서 삭제 연산은 최댓값을 가진 요소를 삭제하는 것이다.
    • 삭제된 루트 노드에는 힙의 마지막 노드를 가져온다.
    • 힙을 재구성한다.
      https://gmlwjd9405.github.io/images/data-structure-heap/maxheap-delete.png
  • 시간 복잡도
    • 힙은 완전 이진트리이므로 전체 높이가 logN으로, 하나의 요소를 힙에 삽입하거나 삭제할 때 힙을 재 정비하는 시간이 logN만큼 소요된다. 총 N개이기 때문에 O(NlongN)이 소요된다.
    • 최선 : O(NlogN)
    • 평균 : O(NlogN)
    • 최악 : O(NlogN)
이름 최선 평균 최악
삽입 N N^2 N^2
선택 N^2 N^2 N^2
버블 N^2 N^2 N^2
퀵 NlogN NlogN N^2
합병 NlogN NlogN NlogN
힙 NlogN NlogN NlogN

7. 기수 정렬(Radix sort)

https://dojinkimm.github.io/assets/imgs/cs/radix_sort.png

8. 셸 정렬

reference